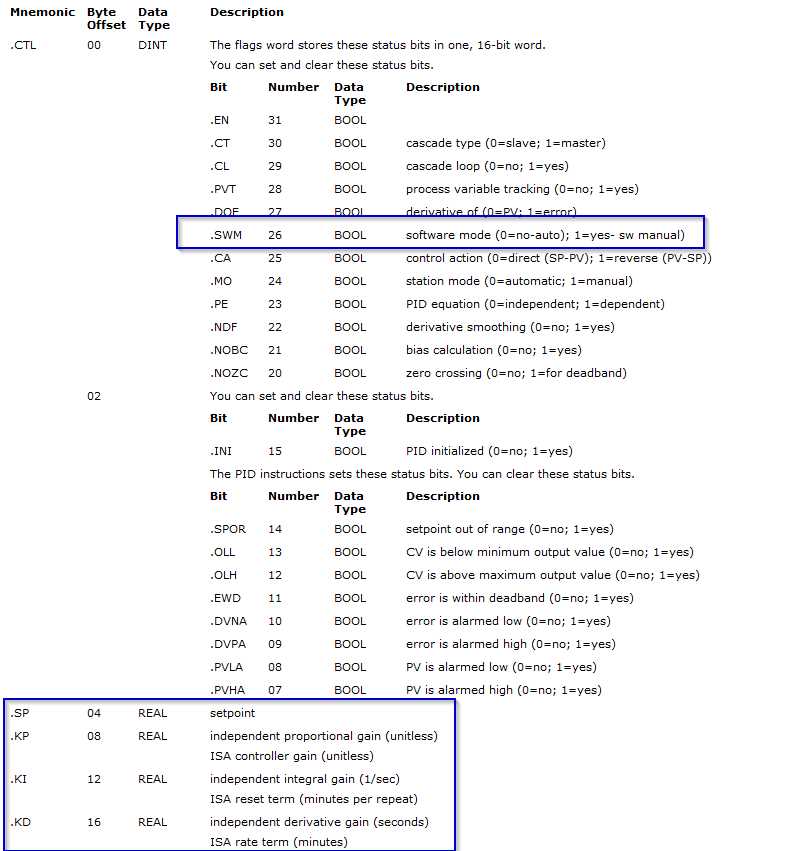
In the realm of automated systems, precise regulation of processes is crucial for maintaining efficiency and achieving optimal performance. This guide delves into the mechanisms of sophisticated control algorithms that are integral to modern industrial automation. By understanding these advanced techniques, professionals can enhance their ability to manage complex systems with greater accuracy and reliability.
Our exploration focuses on the core principles of dynamic regulation, including how to implement and fine-tune algorithms that respond to real-time changes. The ability to adapt and control system variables effectively is essential for ensuring smooth operations and minimizing disruptions. This document provides detailed insights into the processes involved, offering practical knowledge to support efficient system management.
Whether you are seeking to refine existing setups or design new systems from the ground up, mastering these control methodologies will enable you to achieve superior results. The following sections will guide you through the fundamental concepts and applications, equipping you with the expertise needed to excel in the field of process control.
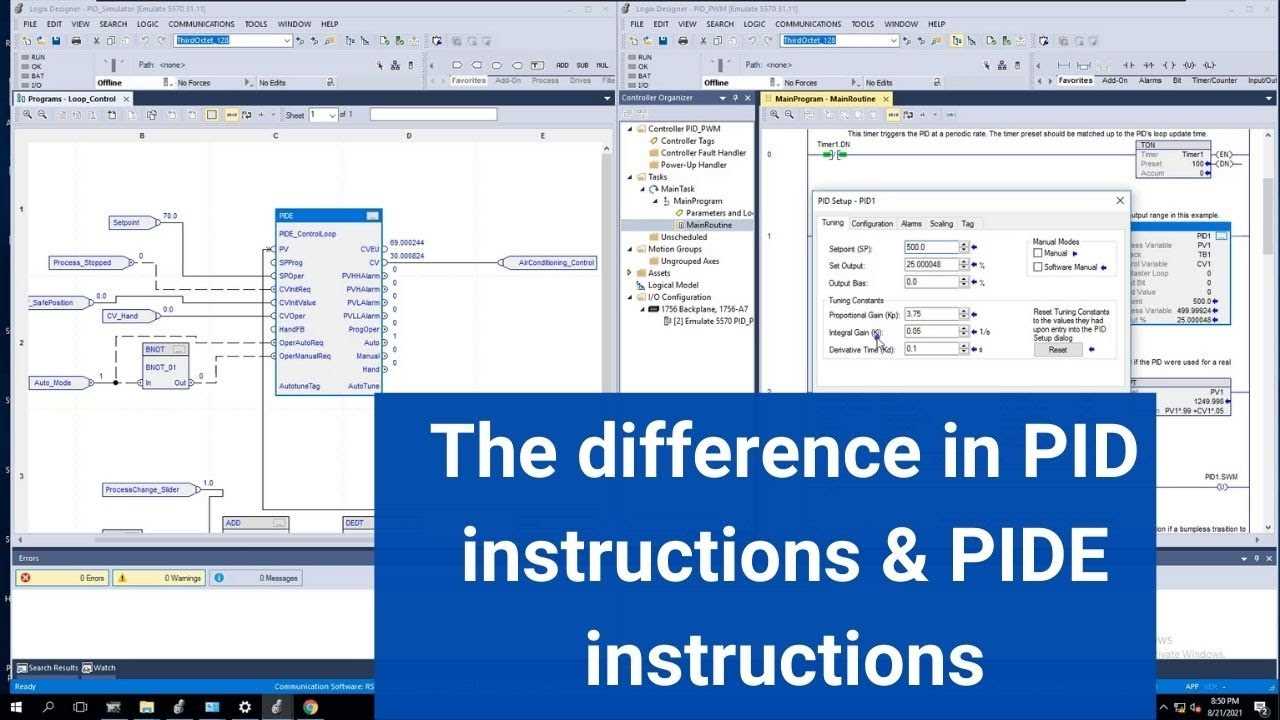
Understanding the Basics of PID Control

At its core, process control involves managing systems to maintain desired outputs despite varying conditions. This is achieved through the application of control algorithms designed to adjust system inputs and maintain stability. One such algorithm is known for its ability to fine-tune control mechanisms by continually adjusting based on feedback, ensuring that a system stays close to its target value.
Proportional-Integral-Derivative control is a method widely used in automated systems to enhance performance. It combines three distinct strategies to respond to deviations from a set point: the proportional element addresses current errors, the integral component corrects past errors, and the derivative part anticipates future errors. This approach allows for precise adjustments, improving the overall accuracy and stability of the system.
By understanding these fundamental elements and how they interact, one can better grasp how automated systems are regulated to achieve optimal performance and reliability.
Overview of RSLogix 5000 PID Instruction
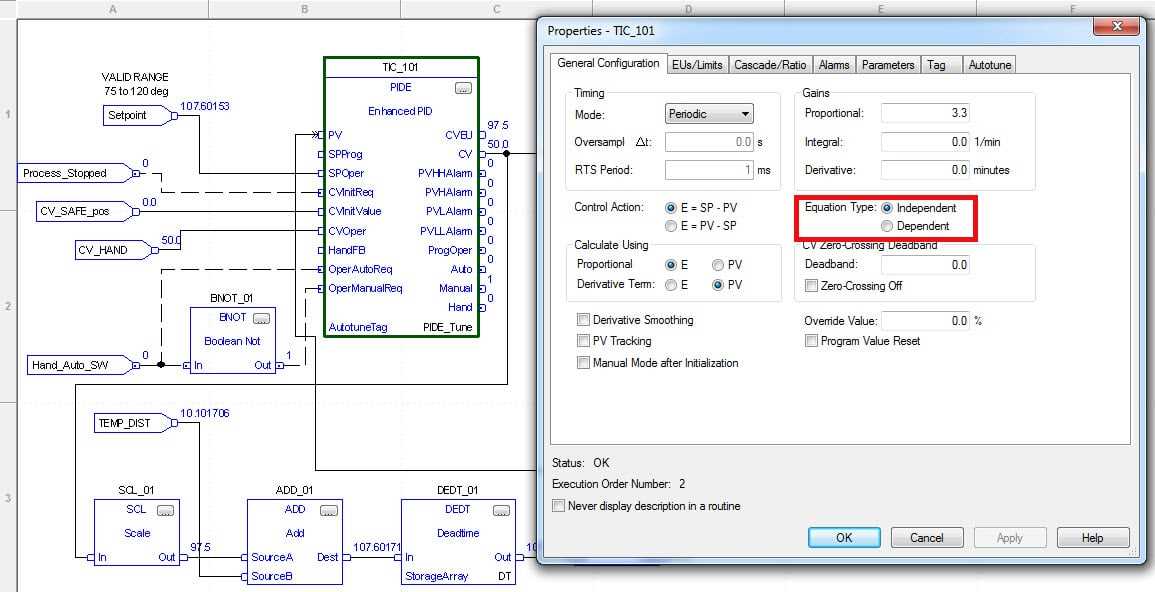
The Proportional-Integral-Derivative (PID) control functionality is essential for maintaining desired system performance in automation processes. This control mechanism dynamically adjusts process variables to achieve and maintain the desired setpoint. The capability to seamlessly integrate this control into automated systems significantly enhances process accuracy and stability.
In this context, the control module provides a robust tool for managing and fine-tuning industrial processes. By employing various control strategies, this functionality allows users to achieve precise control over their systems. The integration process involves configuring specific parameters that dictate how the control actions are performed, ensuring that the system responds optimally to changes and disturbances.
Utilizing this control approach involves setting up parameters that determine the behavior of the control system, including how it reacts to errors and adjustments. The overall goal is to maintain process variables within a desired range, improving both efficiency and reliability. With this tool, users can expect enhanced performance and reduced variability in their automated systems.
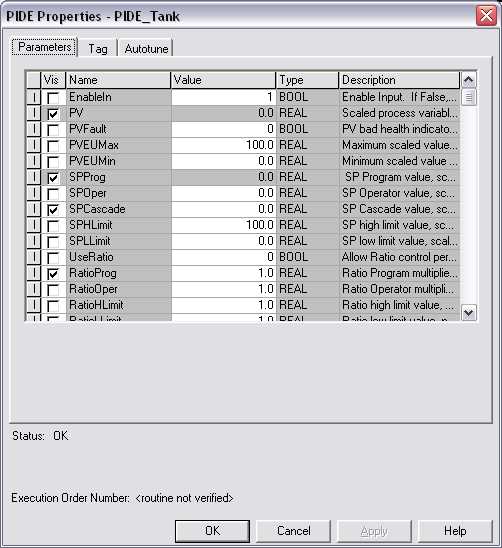
Configuring PID Parameters in RSLogix
Optimizing control loops involves adjusting specific parameters to achieve desired system performance. Proper configuration ensures that the system responds efficiently and maintains stability. This process requires an understanding of various tuning elements that influence how a control system reacts to changes and disturbances.
Understanding Control Parameters
Before diving into configuration, it’s essential to grasp the main components involved:
- Proportional Gain (P): Affects the system’s response to current errors. Higher values lead to faster responses but may cause oscillations.
- Integral Time (I): Influences how the system corrects accumulated past errors. Proper tuning prevents steady-state errors but can introduce lag.
- Derivative Time (D): Determines the system’s response to the rate of error change. It helps in predicting future errors, reducing overshoot and oscillations.
Steps for Tuning Parameters
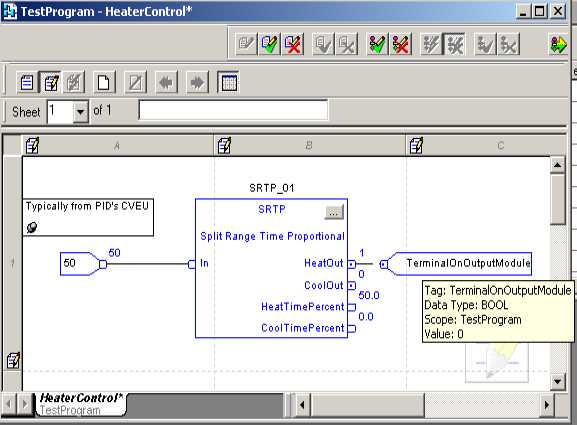
To fine-tune these settings, follow these steps:
- Start with Initial Settings: Begin with default or initial values for all parameters. This provides a baseline for adjustments.
- Adjust Proportional Gain: Gradually increase the proportional gain until the system responds adequately to changes. Watch for oscillations or excessive noise.
- Configure Integral Time: Set the integral time to address steady-state errors. Avoid overly long settings to prevent sluggish responses.
- Refine Derivative Time: Adjust derivative time to manage the response to the rate of error change. Ensure it helps reduce overshoot and does not cause instability.
- Test and Iterate: Observe the system’s behavior and make incremental adjustments as needed. Continuous testing ensures optimal performance and stability.
By following these guidelines, you can effectively configure the parameters to meet your system’s specific needs and achieve optimal control performance.
Common Pitfalls and Troubleshooting Tips
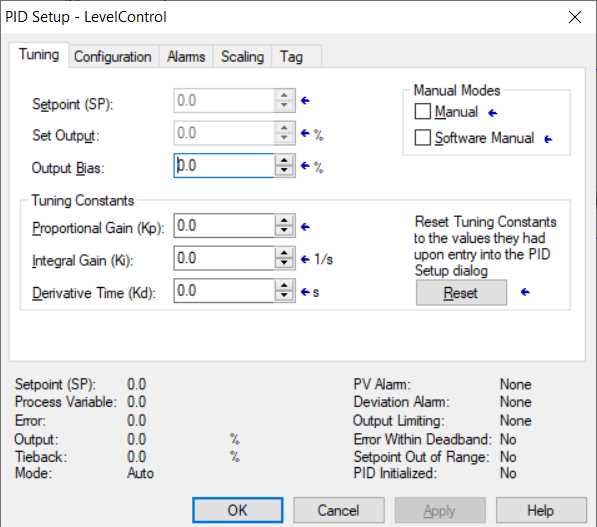
When working with control systems, it’s crucial to be aware of frequent issues that can arise and how to address them effectively. Understanding these common challenges and having strategies to troubleshoot can significantly improve system performance and reliability.
Frequent Issues
- Incorrect Tuning Parameters: One of the most common mistakes is setting inappropriate values for tuning parameters, which can lead to unstable system behavior or poor performance.
- Improper Sensor Calibration: Inaccurate sensor readings can mislead the control logic, causing erratic system responses or ineffective control actions.
- Misconfigured Control Loops: Errors in loop configuration, such as incorrect feedback settings or wrong control strategies, can undermine the effectiveness of the control system.
- Signal Interference: Electrical noise or signal interference can distort sensor signals, leading to incorrect data processing and control decisions.
Troubleshooting Tips
- Verify Parameter Settings: Ensure that all tuning parameters are correctly configured according to the system requirements. Use system documentation or consult with an expert if needed.
- Check Sensor Accuracy: Regularly calibrate sensors and validate their accuracy to prevent faulty readings. Implement calibration routines as part of maintenance procedures.
- Review Loop Configurations: Double-check all settings related to control loops. Ensure that feedback mechanisms and control strategies align with system goals.
- Inspect for Signal Noise: Examine the system for sources of electrical interference. Use shielding or filtering techniques to minimize noise and ensure clean signal transmission.
Advanced Features and Customization Options
In modern control systems, the ability to tailor and enhance functionalities is crucial for achieving optimal performance. This section delves into the advanced features and customization possibilities available within control systems, which allow users to fine-tune their configurations beyond the standard settings. By leveraging these capabilities, operators can achieve more precise control and adapt the system to meet specific needs.
One of the key aspects of customization is the ability to define custom parameters and control strategies. This involves:
- Adjusting the response time of the control loops to better match process dynamics.
- Configuring advanced algorithms that can handle complex control scenarios.
- Implementing specialized functions to enhance system stability and responsiveness.
Furthermore, integration with other system components can be customized to ensure seamless operation. This includes:
- Creating communication links with external devices and systems for data exchange and monitoring.
- Developing custom interfaces for user interaction and control.
- Incorporating feedback mechanisms to adjust settings dynamically based on real-time data.
Another important area is the optimization of control parameters. This can involve:
- Fine-tuning proportional, integral, and derivative gains to enhance performance.
- Utilizing advanced features such as auto-tuning to automatically adjust parameters for optimal operation.
- Employing simulations to predict system behavior and adjust settings accordingly.
Overall, these advanced features and customization options provide the flexibility needed to address specific operational requirements and improve the efficiency of control processes. By exploring and utilizing these capabilities, users can achieve a higher level of control precision and system integration.
Integrating PID with Other Control Systems
Effective integration of control algorithms with various automation systems can greatly enhance operational efficiency and accuracy. When combining a control algorithm with different system components, it is crucial to ensure seamless communication and interoperability. This process often involves adapting the algorithm to work harmoniously with sensors, actuators, and supervisory systems, as well as ensuring that data exchange and feedback loops are well-coordinated.
Combining a control algorithm with supervisory systems requires careful consideration of how data is communicated between the control loop and the supervisory software. It may involve configuring data points and establishing protocols that allow for real-time monitoring and adjustments based on system feedback. Ensuring that the control algorithm can interact effectively with higher-level management systems can lead to improved performance and reliability.
Integrating with sensor and actuator networks involves addressing compatibility issues and ensuring that the control loop receives accurate and timely data from sensors while properly controlling actuators. This might include calibrating sensors, aligning signal formats, and verifying that actuators respond as expected to control signals. Proper integration can optimize process control and enhance overall system responsiveness.
In summary, successful integration of control algorithms with other system components relies on thoughtful configuration and testing. By addressing communication protocols, compatibility, and data accuracy, one can achieve a well-coordinated and efficient control system.
Practical Examples and Case Studies
Understanding how to effectively implement and utilize control systems can be significantly enhanced through real-world examples and detailed case studies. By examining specific scenarios where these systems are applied, users can gain valuable insights into practical applications, troubleshooting techniques, and performance optimization. This section aims to illustrate these concepts with tangible examples, demonstrating how theoretical knowledge translates into operational success.
Case Study 1: Temperature Regulation in a Manufacturing Process
In a large-scale manufacturing plant, maintaining precise temperature control is crucial for product quality and process efficiency. One instance involved optimizing the temperature of an industrial oven used for curing materials. Initially, the temperature fluctuated beyond acceptable limits, resulting in inconsistent product quality. By implementing a well-tuned control strategy, the temperature stability improved significantly. Key adjustments included refining the control parameters and integrating real-time feedback mechanisms. This not only enhanced the consistency of the final product but also reduced energy consumption and operational costs.
Case Study 2: Level Control in a Chemical Processing Facility
In another example, a chemical processing facility needed to manage the level of liquid in a large storage tank. The challenge was to prevent overflows and maintain the desired level with minimal variation. The solution involved designing a control system that could dynamically adjust the inflow and outflow rates based on real-time measurements. By applying advanced tuning techniques and incorporating predictive algorithms, the facility achieved better control over the liquid levels. This resulted in improved safety, reduced waste, and enhanced overall efficiency of the production process.
These case studies highlight how tailored solutions and careful adjustments can address specific challenges in various industrial settings. The practical application of these strategies demonstrates the effectiveness of theoretical knowledge when applied in real-world situations.